回溯算法
回溯算法
1、什么是回溯算法?
回溯在英文中的词是backtracking,回溯算法是外国人发明和命名的,最初翻译到中文的时候会加上一些修饰的意味。牛津词典中对backtrack是这样解释的:to go back along the same route that you have just come along (The path suddenly disappeared and we had to backtrack.),意思就是,沿着来时的路返回去。
回溯算法是一种通过递归探索解空间树来解决问题的算法。其基本思想是通过系统地搜索所有可能的解,在尝试每一个可能的解时,如果发现某个解不可行,则立即回溯并尝试其他可能的解,直到找到所有解或者找到最优解。
归根到底,回溯算法是一种暴力搜索算法,或者叫一种穷举法。
举个例子说一下为什么要有回溯算法。
# 给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
#假设n=100,k=2时,你可能会这么写代码。
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
result = []
for i in range(1,n+1):
for j in range(i+1,n+1):
result.append([i,j])
return result
#假设n=100,k=3,你可能会这么写代码。
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
result = []
for i in range(1,n+1):
for j in range(i+1,n+1):
for k in range(j+1,n+1):
result.append([i,j,k])
return result
#那如果n=100000,k=1000时呢?总不能写1000层for循环吧。
回看一下上面的求解思路,以n=10,k=3举例,我们求解的问题是从[1,10]中找到3个数字的组合,记这个问题为P([1,10],3)。
其实在上面的求解过程中,我们有意无意的在自己的脑海中构建了一颗下面的的树。树的叶子节点是可行解,其他节点是获得可行解的中间步骤。
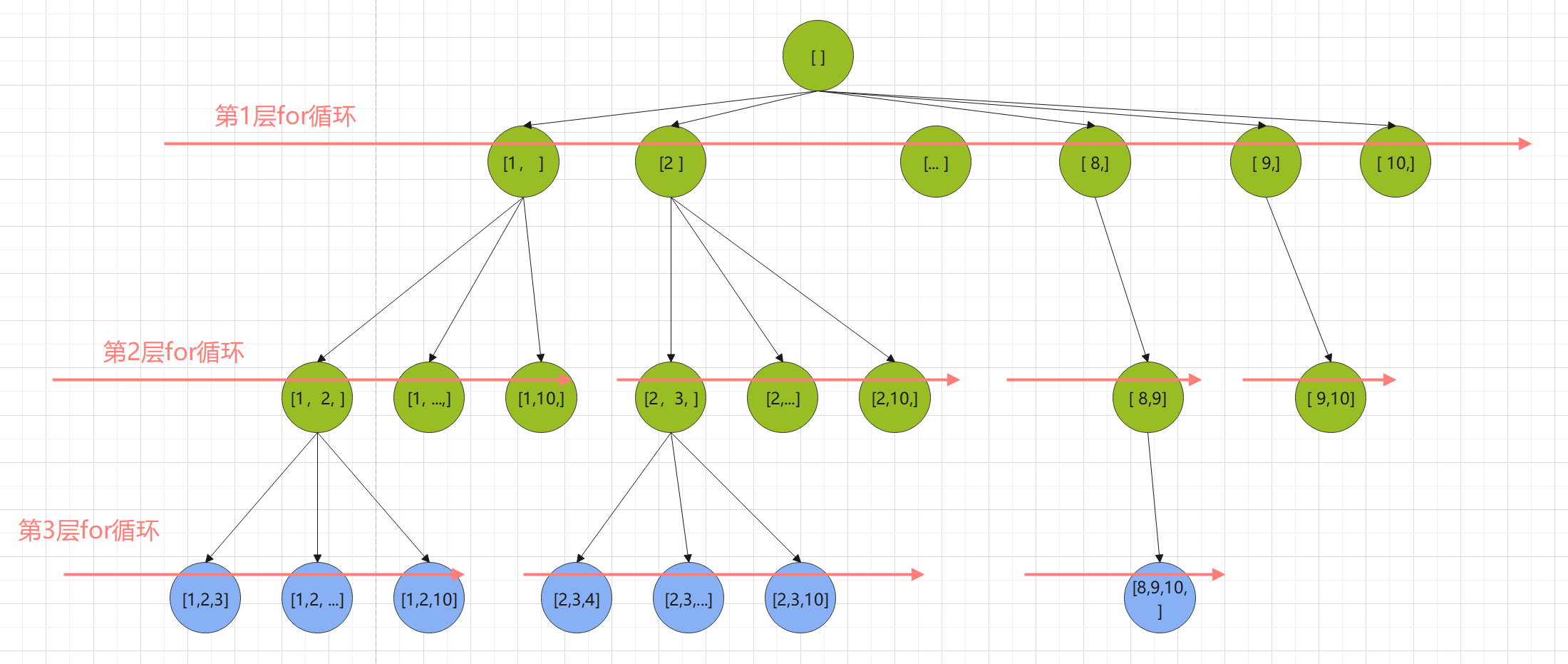
下面我们要解决的是当k比较大时应该怎么让代码去自己探索可行解。下面这幅图展示了我们人类的大脑是如何求解这种组合问题的。尤其是当n和k比较大时,顺序一定是[1,2,3],[1,2,4],[1,2,5]...[1,3,4],[1,3,5],...,[8,9,10]。应该没有人是按照随机顺序来吧。
我们的思考过程应该是这样的。
1、先把1放在结果中形成[1]
2、[1]不是一个可行解,再把2放进去形成[1,2]
3、[1,2]还不是一个可行解,再把3放进去形成[1,2,3]
4、[1,2,3]是可行解了,把这个可行解记录下来。不能再继续往里面放东西了,而是把3拿出去,放一个3后面的数字进来即形成[1,2,4]
5、[1,2,4]是可行解了,把这个可行解记录下来。不能再继续往里面放东西了,而是把4拿出去,放一个4后面的数字进来即形成[1,2,5]
...
[1,2,10]是可行解了,把这个可行解记录下来。不能再继续往里面放东西了,而是把10拿出去,但是10后面没有数字可以放了,我们再把[1,2]下面的可行解探索完了,这时要把2拿出去,换成3
...
下面的图片就展示了上面的过程。
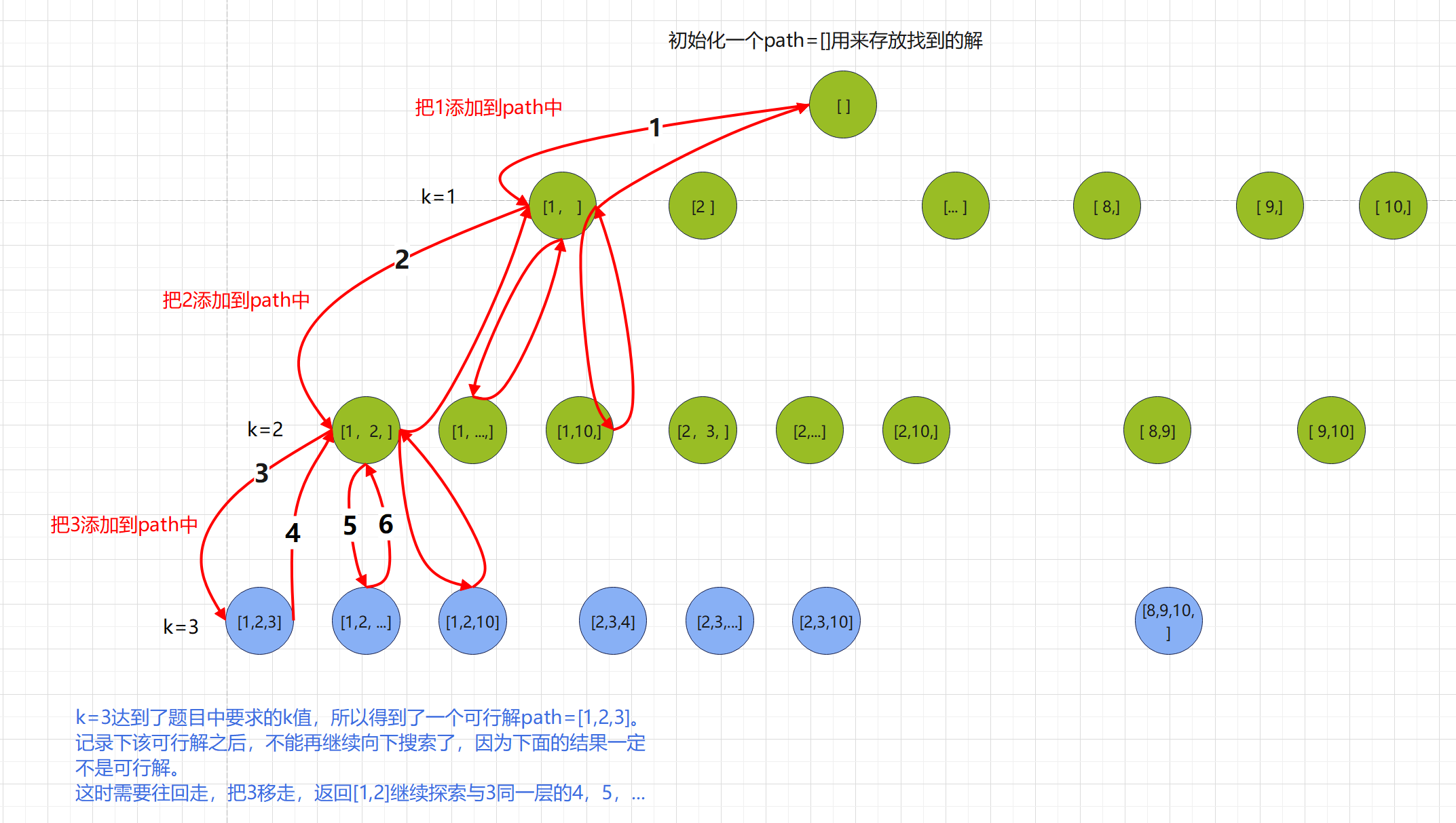
当遇到一个可行解,再这个可行解里面再添加任何东西都不可能是可行解了。此时就需要往回走(把3拿出去),放一个3后面的数字进来即形成[1,2,4]
再看一下英文的解释以及例句(to go back along the same route that you have just come along (The path suddenly disappeared and we had to backtrack.)),是不是就明白是啥意思了。
总结一下,回溯算法就是走不通了就往回走。
2、怎么写回溯算法
回溯算法的核心思想是通过递归探索所有可能的解决方案,并在发现某条路径不符合要求时“回溯”到上一步,尝试其他可能性。回溯算法常用于解决组合、排列、子集等问题。
下面是常用的回溯算法模板,适用于多种问题:
回溯算法模板
def backtrack(路径, 选择列表):
if 满足结束条件:
结果.append(路径) # 找到一个符合条件的解
return
for 选择 in 选择列表:
# 做选择
路径.append(选择)
# 递归探索新的选择
backtrack(路径, 新的选择列表)
# 撤销选择(回溯)
路径.pop()
关键步骤解释:
- 路径:当前已经做出的选择或结果的部分解(也就是中间过程)。
- 选择列表:可以做出的选择,即在当前路径下还可以选择的元素。
- 结束条件:当找到一个符合要求的解时,递归终止,记录该解并返回。
- 做选择:选择一个元素,将其加入路径,并从剩下的可选元素中继续递归。
- 递归探索:递归调用
backtrack(),不断尝试新的选择,进入更深的路径。 - 撤销选择:通过
pop()操作将之前的选择撤销,回溯到上一步,以便尝试其他选择。
这是回溯算法的一个标准模板,一开始可能不熟练,多加练习就好了。
3、回溯算法实例
这一部分,我们用leetcode中有关回溯算法的题目来看看回溯算法到底怎么应用于求解问题中。
17. 电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。

示例 1:
输入:digits = "23"
输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
示例 2:
输入:digits = ""
输出:[]
示例 3:
输入:digits = "2"
输出:["a","b","c"]
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
#首先,我们应该初始化一个数字与字母对应的表,让代码知道哪个数字对应着哪些字母
a_dict={
"2":["a","b","c"],
"3":["d","e","f"],
"4":["g","h","i"],
"5":["j","k","l"],
"6":["m","n","o"],
"7":["p","q","r","s"],
"8":["t","u","v"],
"9":["w","x","y","z"]
}
#初始化一个result数组用来存放最终结果
result = []
def backtrack(path, index):
if len(path) == len(digits):
result.append("".join(path)) # 找到一个符合条件的解,把他连成字符串后存在result中
return
for s in a_dict[digits[index]]:
# 做选择
path.append(s)
# 递归探索新的选择
backtrack(path, index+1)
# 撤销选择(回溯)
path.pop()
backtrack([],0)
return result
22. 括号生成
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例 1:
输入:n = 3
输出:["((()))","(()())","(())()","()(())","()()()"]
示例 2:
输入:n = 1
输出:["()"]
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
#初始化一个result数组用来存放最终结果
result = []
#这个题我们应该考虑什么是可行解,也就是终止条件是什么。
#第一个条件就是必须有2*n个半括号,第二个条件就是在任何时候右括号的数量不能超过左括号。
def backtrack(path: str, left: int, right: int):
if left < right or left>n:
return
if len(path) == 2 * n:
result.append("".join(path))
return
for i in ["(",")"]:
path.append(i)
if i=="(":
backtrack(path,left+1,right)
else:
backtrack(path,left,right+1)
path.pop() # 回退,移除上一个选择
backtrack([],0)
return result
39. 组合总和
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
result = []
n = len(candidates)
candidates.sort()
def bt(path,start):
if sum(path) > target:
return
if sum(path) == target:
result.append(path[:])
return
for i in range(start,n):
path.append(candidates[i])
bt(path,i)
path.pop()
bt([],0)
return result
40. 组合总和 II
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
**注意:**解集不能包含重复的组合。
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
result = []
n = len(candidates)
candidates.sort()
# print(candidates)
def backtracking(path,start):
if sum(path)==target:
result.append(path[:])
return
if sum(path)>target:
return
for i in range(start,n):
if i > start and candidates[i] == candidates[i - 1]:
continue
path.append(candidates[i])
backtracking(path,i+1)
path.pop()
backtracking([],0)
return result
46. 全排列
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
result = []
n = len(nums)
def backtracking(path,travelled):
if len(path) == n:
result.append(path[:])
return
for i in range(0,n):
if i in travelled:
continue
travelled.append(i)
path.append(nums[i])
backtracking(path,travelled)
path.pop()
travelled.pop()
backtracking([],[])
return result
47. 全排列 II
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2]
输出:
[[1,1,2],
[1,2,1],
[2,1,1]]
示例 2:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
result = []
n = len(nums)
nums.sort()
used = [False] * n
def backtracking(path):
if len(path) == n:
result.append(path[:])
return
for i in range(0,n):
if used[i]:
continue
if i>0 and nums[i] == nums[i-1] and not used[i-1]:
continue
used[i] = True
path.append(nums[i])
backtracking(path)
path.pop()
used[i] = False
backtracking([])
return result
77. 组合
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
示例 1:
输入:n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
示例 2:
输入:n = 1, k = 1
输出:[[1]]
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
result = []
def backtracking(path,start):
if len(path) == k:
result.append(path[:])
return
for i in range(start,n+1):
path.append(i)
backtracking(path,i+1)
path.pop()
backtracking([],1)
return result
78. 子集
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的
子集
(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
result = []
n = len(nums)
def backtracking(path,start):
if len(path)<=n:
result.append(path[:])
# return
for i in range(start,n):
path.append(nums[i])
backtracking(path,i+1)
path.pop()
backtracking([],0)
return result
79. 单词搜索
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
class Solution:
def exist(self, board: List[List[str]], word: str) -> bool:
m, n = len(board), len(board[0])
travelled = [[False] * n for _ in range(m)]
def isinarea(r: int, c: int) -> bool:
return 0 <= r < m and 0 <= c < n
def backtracking(r: int, c: int, index: int) -> bool:
if index == len(word): # 找到完整的单词
return True
if not isinarea(r, c) or travelled[r][c] or board[r][c] != word[index]:
return False
# 标记为已访问
travelled[r][c] = True
# 递归检查四个方向
found = (backtracking(r + 1, c, index + 1) or
backtracking(r - 1, c, index + 1) or
backtracking(r, c + 1, index + 1) or
backtracking(r, c - 1, index + 1))
# 恢复状态
travelled[r][c] = False
return found
for i in range(m):
for j in range(n):
if backtracking(i, j, 0): # 从每个单元格开始
return True
return False
89.格雷码
n 位格雷码序列 是一个由 2n 个整数组成的序列,其中:
- 每个整数都在范围
[0, 2n - 1]内(含0和2n - 1) - 第一个整数是
0 - 一个整数在序列中出现 不超过一次
- 每对 相邻 整数的二进制表示 恰好一位不同 ,且
- 第一个 和 最后一个 整数的二进制表示 恰好一位不同
给你一个整数 n ,返回任一有效的 n 位格雷码序列 。
示例 1:
输入:n = 2
输出:[0,1,3,2]
解释:
[0,1,3,2] 的二进制表示是 [00,01,11,10] 。
- 00 和 01 有一位不同
- 01 和 11 有一位不同
- 11 和 10 有一位不同
- 10 和 00 有一位不同
[0,2,3,1] 也是一个有效的格雷码序列,其二进制表示是 [00,10,11,01] 。
- 00 和 10 有一位不同
- 10 和 11 有一位不同
- 11 和 01 有一位不同
- 01 和 00 有一位不同
示例 2:
输入:n = 1
输出:[0,1]
#此代码只能运行n=9的情况,n>9会超时
class Solution:
def grayCode(self, n: int) -> List[int]:
result =[]
used = [False]*2**n
def hasExactlyOneBitDifferent(a: int, b: int) -> bool:
x = a ^ b # 计算异或
return x != 0 and (x & (x - 1)) == 0
def backtracking(path):
if len(path)>=2 and not hasExactlyOneBitDifferent(path[-1],path[-2]):
return
if len(path) == 2**n and hasExactlyOneBitDifferent(path[0],path[-1]):
result.append(path[:])
return
for i in range(1,2**n):
if used[i]:
continue
path.append(i)
used[i] = True
backtracking(path)
if result:
return
path.pop()
used[i] = False
# return result[0]
backtracking([0])
return result[0]
90. 子集 II
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的
子集
(幂集)。
解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
示例 1:
输入:nums = [1,2,2]
输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
result = []
n = len(nums)
nums.sort()
def backtracking(path,start):
result.append(path[:])
for i in range(start,n):
if i>start and nums[i]== nums[i-1]:
continue
path.append(nums[i])
backtracking(path,i+1)
path.pop()
backtracking([],0)
return result

